|
2.1. Необходимые и достаточные условия поиска безусловного экстремума
Задачи поиска безусловного экстремума имеют огромное значение в теории оптимизации, т.к. большинство задач на условный экстремум сводятся, путем замены целевой функции, к задачам поиска безусловного экстремума.
Рассмотрим сначала случай функции
одной переменной: Пусть для определенности точка
Рассмотрим:
Для того чтобы точка
Рассмотрим правую часть выражения
(2). Так как рассматривается достаточно малая
Если это условие выполняется, то
следующим слагаемым, оказывающим влияние на знак левой части (2), оказывается
2-е слагаемое. Очевидно, что это слагаемое будет положительным, если
Аналогично, для случая функции
многих переменных, если точка
Так же как и в случае одной переменной:
и, следовательно, для того чтобы
точка
Аналогично, для того чтобы точка
Т.о. можно сформулировать необходимые и достаточные условия безусловного экстремума.
Теорема 1. (о необходимых условиях экстремума (НУ)) Если точка
Замечание.
Точки, в которых выполняются необходимые условия безусловного экстремума
функции
Теорема 2. (о необходимых условиях экстремума 2-го порядка (НУ 2-го порядка)) Если точка
Теорема 3. (о достаточных условиях безусловного экстремума (ДУ)) Если функция
Алгоритм решения задачи поиска безусловного экстремума с использованием необходимых и достаточных условий
Исследование
знакоопределенности матрицы ·
·
·
·
·
Дано:
Решение:
1. Градиент
функции:
2.
3. Решаем
систему: Таким образом
получена стационарная точка функции:
4. Матрица Гессе:
5.
6. Исследуем знакоопределенность матрицы по критерию Сильвестра:
В точке А :
значит
Ответ: найдена
точка локального минимума функции Пример 2.2. Найти экстремумы в задаче
Дано:
Решение:
1. Градиент
функции:
2.
3. Решаем
систему: Таким образом
получена стационарная точка функции:
4. Матрица Гессе:
5.
6. Исследуем знакоопределенность матрицы по критерию Сильвестра:
В точке А: значит достаточные условия экстремума в точке не выполняются.
Проверим необходимые условия экстремума 2-го порядка, вычислив собственные числа :
значит матрица
Дополнительная проверка. Т.к. значение
функции
Ответ: найдена
точка локального минимума функции
|

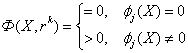 (2)
(2)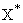
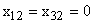 .
.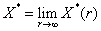 .
.