2.2.1.2.  Метод градиентного наискорейшего спуска

 

Алгоритм метода:  

здесь

•  - направление антиградиента функции;
• - шаг вычисляется из условия наибольшего убывания функции в точках последовательности, построенной по закону: .

 

Геометрическая интерпретация метода

 

Как видно из чертежа, точка  принимает на направлении спуска предельное положение, которое характеризуется тем, что линия уровня, проходящая через точку , касается направления спуска, а, следовательно, в точках минимизирующей последовательности, построенной по методу градиентного наискорейшего спуска, выполняется условие:

.

 

Критерии окончания метода такие же, как и в методе градиентного спуска.

Начальными параметрами метода являются:  (дополнительно или ).

 

Вычисление шага может быть выполнено тремя способами:

 

Способ A заключается в вычислении функции , эта функция оказывается функцией одной переменной , т.е. , и последующем использовании необходимых и достаточных условий безусловного экстремума этой функции: . Этот способ может быть использован в случаях, когда функция достаточно проста.

Способ B заключается в использовании условия перпендикулярности градиентов в точках последовательности для вычисления шага. Способ также может быть использован в случаях, когда функция достаточно проста.

 

Способ C предполагает численное решение задачи методами одномерной минимизации [1] на отрезке  с заданной точностью .  Этот способ используется при компьютерной реализации метода.

 

Пример 2.4.

 

Дано: .

Сделать 1 итерацию методом градиентного спуска из начальной точки .

 

Решение:

 

Итерация 0 алгоритма (соответствует начальной точке)

 

;

;

;                      .

 

Итерация 1 алгоритма ()

 

Способ A  вычисления шага .

 

Вычислим значение функции в точке : .

 

Как видно функция в точке зависит только от величины шага , следовательно, можно записать: .

 

Найдем минимум функции :

 - значение шага;

- значит, функция принимает минимальное значение.

 

Окончательно:

 

;      ;

 

;                       .

 

Способ B вычисления шага .

 

Вычислим градиент функции в точке :

 

.

Воспользуемся условием :

.

 

Окончательно:

 

;      ;

 

;                       .
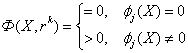
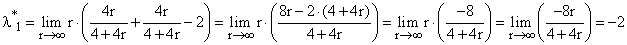