2.2.1.4. Метод Гаусса-Зейделя (наискорейшего покоординатного спуска)

 

Алгоритм метода:

здесь:

q  - проекция на ось  антиградиента функции;

q  - шаг вычисляется из условия наибольшего убывания функции в точках последовательности, построенной по закону (4.1): .

 

Направление оси для проекции антиградиента может меняться циклически, например: на итерации №1 – ось , на итерации №  2 – ось  и т.д., на итерации № n – ось , на итерации № n+1 – ось .

 

Геометрическая интерпретация метода

 

 

Критерии окончания метода такие же, как и в методе градиентного спуска.

Начальными параметрами метода являются:  (дополнительно или ).

 

Вычисление шага  может быть выполнено способами A и C, описанными в методе градиентного наискорейшего  спуска.

 

Пример 2.5.

 

Дано: .

Сделать 2 итерации методом Гаусса-Зейделя из начальной точки .

 

Решение:

 

Итерация 0 алгоритма (соответствует начальной точке) – см. пример 2.1.

 

Итерация 1 алгоритма (k=0)

 

.

 

Для проекции градиента выберем направление оси .

.

 

Вычислим значение функции в точке : .

Как видно функция в точке зависит только от величины шага , следовательно, можно записать: .

 

Найдем минимум функции :

 - значение шага;

- значит, функция принимает минимальное значение.

;                        ;

;                                   .

 

Итерация 2 алгоритма (k=1)

 

 

Для проекции градиента выберем направление оси .

.

 

Вычислим значение функции в точке :

 

Найдем минимум функции :

 - значение шага;

- значит, функция принимает минимальное значение.

;               ;

;                                  .

 

 

Сходимость  метода  градиентного спуска (градиентного наискорейшего спуска, покоординатного спуска и метода Гаусса-Зейделя) регламентируется теоремой.

 

Теорема.

Если функция ограничена снизу, а ее градиент удовлетворяет условию Липшица:

,

то метод градиентного спуска гарантирует  при .

 

Поскольку критерий окончания гарантирует выполнение в точке только необходимых условий минимума, но не достаточных, можно утверждать, что метод обеспечивает сходимость к стационарной точке функции, в которой необходимо проверить достаточные условия минимума.

 

Сходимость именно к точке минимума гарантируется только для выпуклых функций.
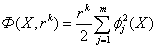
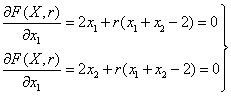