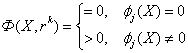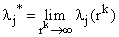2.2.2. Методы второго порядка

 

2.2.2.1. Метод Ньютона

 

Алгоритм метода:  

здесь:

•  - направление спуска;
• .

 

 

Геометрическая интерпретация метода для квадратичной функции: 

 

 

Покажем это.

Аппроксимируем функцию квадратичной функцией в окрестности точки . Для этого разложим функцию в окрестности этой точки в ряд Тейлора и ограничимся рассмотрением трех слагаемых ряда:

 

  

Здесь выступает в роли приращения аргумента.

 

Тогда аппроксимирующая функция имеет вид:

Поставим следующую задачу: найти такое приращение аргумента , при котором  примет минимальное значение. Для решения задачи воспользуемся необходимыми и достаточными условиями минимума:

 

;

.

Следовательно, если , то при  функция имеет минимум.

 

Таким образом, решение задачи методом Ньютона предполагает построение последовательности минимумов аппроксимирующих квадратичных функций .

Соответственно, в случае, когда функция является квадратичной, построенная в любой точке аппроксимирующая функция  совпадет с , а значит, метод Ньютона при отыщет ее минимум за один шаг.

 

Геометрическая интерпретация метода: 

 

  

Критерии окончания метода такие же, как и в методе градиентного спуска.

Начальными параметрами метода являются:  (дополнительно или ).

 

Сходимость метода Ньютона. Сходимость метода Ньютона доказана только для сильно выпуклых функций и существенно зависит от выбора начальной точки . Можно утверждать, что метод Ньютона обеспечивает сходимость к точке минимума функции, только при условии выполнения условия  в каждой точке последовательности .

 

Пример 2.7.

Дано:

Сделать 1 итерацию методом Ньютона из начальной точки

 

Решение:

 

Итерация 0 алгоритма (соответствует начальной точке)

;              

;                     

 

Найдем обратную матрицу:

·        

·        

·        

·        

 

Итерация 1 алгоритма ()

Вычислим значение функции в точке :

;                      

Очевидно, что на 1-й итерации найдены координаты стационарной точки с точностью .