3.1.3. Необходимые и достаточные условия экстремума. Метод множителей Лагранжа

 

 

Определение 3.1.

Функция  называется классической функцией Лагранжа.

Функция зависит от  переменных:  штук и  штук  - называемых множителями Лагранжа.

 

Определение 3.2.  Вторым дифференциалом функции Лагранжа называется функция:

Определение 3.3. Первым дифференциалом ограничения  называется функция:

 

Теорема 1.  (о необходимых условиях экстремума)

 

Пусть  есть точка локального условного экстремума в задаче *, и при этом  являются линейно-независимыми, то найдутся такие , что:

·          (условие стационарности функции Лагранжа по)

·          (условие допустимости решения)

 

Теорема 2.  (о достаточных условиях экстремума)

 

Если в точке выполняются необходимые условия экстремума и  при всех ненулевых , таких, что , то - точка условного локального минимума функции, если же при всех тех же условиях , то - точка условного локального максимума функции.

 

 

 

Алгоритм решения задачи методом множителей Лагранжа:

 

1. Записать классическую функцию Лагранжа: . 2.  Записать необходимые условия экстремума ФМП при ограничениях типа равенств:   3. Решить полученную систему. Решение системы – условно-стационарные точки .   4. Проверить достаточные условия экстремума в каждой точке , для этого Записать второй дифференциал функции Лагранжа: . Записать дифференциалы ограничений . В каждой точке : 4.1. Вычислить второй дифференциал .   4.2. Записать условия равенства 0 дифференциалов ограничений в каждой точке :     4.3. Используя уравнения из п. 4.2, выразить любые  дифференциалов переменных через оставшиеся и подставить их в выражение для .   4.4. Определить знак : ·         если  при , то точка  - точка условного  локального минимума в задаче; ·         если  при , то точка  - точка условного локального максимума в задаче.

 

Пример 3.3.

 

Дано:

 

Найдем решение задачи методом множителей Лагранжа.

Здесь ограничение должно  быть переписано в виде:

Решение:

 

1. Запишем функцию Лагранжа: .

2. Запишем необходимые условия экстремума.

3. Найдем координаты условно-стационарных точек.

Получена условно-стационарная точка  

 

4. Установим тип полученной точки с помощью достаточных условий экстремума.

 

Составляем второй дифференциал функции Лагранжа:

 

 

Составляем дифференциал ограничения:

 

 

В точке  имеем:  при условии .

Значит , тогда получим  при , следовательно, точка A – условный локальный минимум.

 

Ответ: получена точка - условный локальный минимум.

 

 Пример 3.4.

 

Дано:

Найти решение задачи методом множителей Лагранжа.

Здесь ограничение должно  быть переписано в виде:

Решение:

1. Запишем функцию Лагранжа:

 

2. Запишем необходимые условия экстремума.

3. Найдем координаты условно-стационарных точек.

Получены две точки и

 

4. Установим тип полученной точки с помощью достаточных условий экстремума.

 

Составляем второй дифференциал функции Лагранжа:

 

 

Составляем дифференциал ограничения:

 

 

В точке :

 при условии ,

получим  при , следовательно, точка  – условный локальный максимум.

 

В точке :

 при условии ,

получим  при , следовательно, точка – условный локальный минимум.

 

Ответ: получены точка 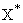- условный локальный максимум и точка - условный локальны минимум.