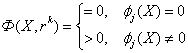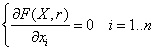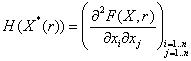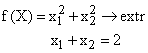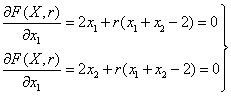3.1.4. Метод штрафной функции

 

Метод штрафной функции относится к численным методам решения задачи *.

 

Метод штрафной функции предусматривает поиск решения задачи в результате решения последовательности задач безусловной минимизации вида:

,              **                                                   

здесь    - вспомогательная функция

 - штрафная функция

 - штрафной параметр, при решении каждой задачи ** фиксируется

 

Штрафная функция конструируется из условия:

причем, чем больше , тем больше штраф. Кроме того, штраф должен быть таким, чтобы при  штраф  при невыполнении ограничений, т.е. становился тем больше, чем больше не выполняются ограничения.

Обычно, в качестве штрафной используют функцию вида:

Идея метода штрафной функции: при каждом значении  ищется точка  минимума в задаче ** при заданном значении параметра с помощью одного из методов безусловной минимизации. Полученная точка используется в качестве начальной в следующей задаче **  при  возрастающем значении параметра .

Доказано, что при , последовательность получаемых точек  стремится к :

 

Существует связь между значением параметра штрафа  и множителями Лагранжа:

 

Замечание. В случае поиска условного экстремума квадратичной функции при линейном ограничении задача ** может быть решена аналитически.

 

Алгоритм аналитического решения задачи методом штрафной функции:

 

 

1. Записать вспомогательную функцию: 2. Записать необходимые условия экстремума для вспомогательной функции: 3. Найти решение полученной системы: . Решение системы зависит от параметра . 4. Найти условно-стационарную точку в задаче: . 5. Составить матрицу Гессе для вспомогательной функции: 6. Исследовать знакоопределенность матрицы при по критерию Сильвестра.   7. Записать оценку множителей Лагранжа: .

 

Замечание.

В случае поиска максимума, используют вспомогательную функцию вида:

и оценку множителей Лагранжа вычисляют по формуле:

 

Пример 3.5.

 

Дано:

 

Найдем решение задачи методом штрафной функции.

Здесь ограничение должно  быть переписано в виде:

Решение:

1. Запишем вспомогательную функцию: .

 

2. Запишем необходимые условия экстремума.

 

3. Найдем координаты стационарных точек вспомогательной функции:

Получена условно-стационарная точка .

 

4. Найдем координаты условно-стационарных точек.

, следовательно, получена условно-стационарная точка   .

 

5. Составим матрицу Гессе для вспомогательной функции:.

 

6. По критерию Сильвестра:  при                                                                                                               при ,

значит матрица  и точка  - условный минимум.

 

7. Запишем оценку множителя Лагранжа:

Ответ: получена точка - условный локальный минимум.