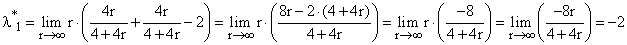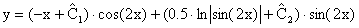Методы оптимизации
3.2.1. Необходимые и достаточные условия экстремума. Метод множителей Лагранжа
|
3.2.1. Необходимые и достаточные условия экстремума. Метод множителей Лагранжа
Определение 3.1. Ограничение
Определение 3.2. Ограничение
Теорема 1. (о необходимых условиях экстремума)
Пусть ·
·
·
или
·
Теорема была доказана Куном и Таккером, и в литературе встречается под названием теорема Куна-Таккера.
В отличие от случая ограничений типа равенств, необходимые условия экстремума формулируются отдельно для минимума и для максимума.
Теорема 2. (о достаточных условиях экстремума первого порядка)
Пусть в точке
Теорема 3. (о достаточных условиях экстремума второго порядка)
Если в точке ·
·
то
Алгоритм решения задачи методом множителей Лагранжа
1. Записать
классическую функцию Лагранжа: 2.
Записать необходимые условия экстремума ФМП при ограничениях типа неравенства:
3. Решить
полученную систему полным перебором вариантов: ограничение Решения
системы – условно-стационарные точки
Замечание. Если точка
4. Отбраковка. Из рассмотрения исключить точки, не принадлежащие множеству допустимых решений. Из
рассмотрения исключить точки, для которых
5. Проверить
достаточные условия экстремума первого порядка в каждой оставшейся точке
6. Для
оставшихся точек Записать
второй дифференциал функции Лагранжа: Записать
дифференциалы ограничений В каждой
точке 6.1. Вычислить
второй дифференциал
6.2. Записать
условия, накладываемые на дифференциалы активных ограничений в каждой точке •
•
Замечание.
Если в точке все ограничения пассивны, то исследуется знак
6.3.
Используя уравнения и (или) неравенства из п. 6.2, выразить любые дифференциалы
переменных через оставшиеся и подставить их в выражение для 6.4.
Определить знак •
если •
если
Дано:
Найти решение задачи методом множителей Лагранжа.
Здесь ограничения должны быть переписаны в виде: Решение:
1. Запишем функцию Лагранжа:
2. Запишем необходимые условия экстремума.
3. Найдем координаты условно-стационарных точек.
Случай а)
Случай б)
Случай в)
г)
4. Отбракуем лишние точки:
Исключаем точку
5. Проверим ДУ 1-го
порядка: в точках
6. Установим тип полученных точек с помощью ДУ 2-го порядка.
Составляем второй дифференциал функции Лагранжа:
Составляем дифференциалы ограничений:
Точка Имеем получим
Точка Имеем получим
Ответ: получена точка
Дано:
Найти решение задачи методом множителей Лагранжа.
Здесь ограничения должны быть переписаны в виде: Решение: 1. Запишем функцию Лагранжа:
2. Запишем необходимые условия экстремума.
3. Найдем координаты условно-стационарных точек.
Случай а)
Случай б)
Случай в)
г)
4. Отбракуем лишние точки:
Из оставшихся точек:
5. Проверим ДУ 1-го
порядка: в точках В точке В точке
6. Установим тип оставшихся точек
Составляем второй дифференциал функции Лагранжа:
Составляем дифференциалы ограничений:
Точка Тогда
Точка Тогда получим
Точка Тогда получим
Ответ: получена
точка
|

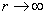
 при
при 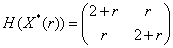 при
при