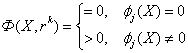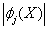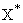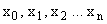4.1. Графическое решение задачи

 

В случае двух переменных, поставленные задачи могут быть решены графически.

 

Алгоритм графического решения задачи

 

1. Построить множество допустимых решений, задаваемое ограничениями.   2. Построить градиент целевой функции в точке .   3. Построить линию уровня целевой функции, проходящую через точку .   Если, построенная линия уровня не имеет общих точек с множеством допустимых решений, то, используя параллельный перенос, построить еще одну линию уровня функции, пересекающую множество допустимых решений. Линию уровня, имеющую общие точки с множеством допустимых решений, отметим .   4. Для поиска максимума целевой функции переносить, используя параллельный перенос,  построенную линию уровня  в направлении градиента до последнего касания с множеством допустимых решений. В точке (точках) касания достигается условный максимум. Если множество допустимых решений в направлении градиента неограниченное, то максимума в задаче нет.   Для поиска минимума целевой функции аналогично переносить построенную линию уровня  в направлении, противоположном градиенту, до последнего касания с множеством допустимых решений. В точке (точках) касания достигается условный минимум. Если множество допустимых решений в направлении, противоположном  градиенту, неограниченное, то минимума в задаче нет.

 

При графическом решении задачи возможны следующие варианты:

• в случае A – решение единственное (точка )
• в случае B – бесконечное множество решений (на отрезке )
• в случае C – решение нет, так как область допустимых решений в направлении поиска решения незамкнута
• в случае D – решений нет, так как ограничения в задаче несовместны.

 

 

 

Пример 4.1.

 

Дано:

 

Найдем решение задачи графически.

 

Решение:

 

1. МДР, определяемое ограничениями, выделено на чертеже.

2. Градиент функции имеет вид . Построим его на чертеже.

3. Уравнение линии уровня функции имеет вид: .

Уравнение линии уровня функции в точке : . Построим ее на чертеже.

 

4. Задача имеет бесконечное множество решений на отрезке ,  здесь , .

 

Дано:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение

 

1. Для графического решения задачи построим множество допустимых решений, задаваемое ограничениями (1)-(3).

 

Ограничение (1) в задаче определяется прямой   , проходящей через точки:

Множество допустимых решений в задаче будет ограничено этой прямой и НЕ будет содержать точку  , т.к. при подстановке координат этой точки в ограничение (1) получается верное неравенство:

 

Ограничение (2) в задаче определяется прямой   , проходящей через точки:

 

Множество допустимых решений в задаче будет ограничено этой прямой и будет содержать точку  , т.к при подстановке координат этой точки в ограничение (2) получается верное неравенство:

 

Ограничения (3) в задаче задают  1-ю четверть координатной плоскости.

 

Отметим крайние точки получившегося множества: B, С.

 

Построим градиент функции  в точке с координатами

 

Построим линию уровня функции , проходящую через точку с координатами . Для этого найдем значение константы , подставив координаты точки в целевую функцию: , и затем построим прямую .

 

Будем искать точку максимума функции как последнюю точку касания линии уровня функции и множества допустимых решений в направлении градиента функции. Как видно из чертежа такой точки не существует, т.к. множество допустимых решений в направлении градиента незамкнуто, следовательно, максимума в задаче нет.

 

Будем искать точку минимума функции как первую точку касания линии уровня функции и множества допустимых решений в направлении градиента функции. Как видно из чертежа, это точка . Таким образом, получено решение задачи поиска минимума функции:

 

Как видно из чертежа, это точки отрезка , где , . Таким образом, получено решение задачи поиска максимума функции: