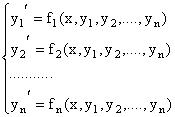4.2. Симплекс метод Данцига

Рассмотрим решение канонической задачи

Решается задача:       

                                                                                                *

                                                                                                                 **

Множество допустимых решений в задаче, определяемое ограничениями  * и **, есть выпуклое множество, которое в случае двух переменных геометрически представляет собой выпуклый многогранник, имеющий конечное число крайних точек.

Определение 4.1. Крайней точкой выпуклого множества X называется точка X, которая не может быть выражена в виде выпуклой комбинации других точек X, . В случае двух переменных, крайняя точка X, это точка, которая не может принадлежать отрезку, соединяющему две другие произвольные точки множества X.

Теорема 1. Если функция в задаче достигает максимума на множестве X, определяемом ограничениями, то она достигает его, по крайней мере, в одной из крайних точек этого множества. Если она достигает его в нескольких крайних точках, то она достигает его на любой выпуклой комбинации этих крайних точек.

Определим понятие базисное решение системы линейных уравнений.

Преобразуем систему уравнений  к виду, при котором некоторые  переменных входят только в одно из уравнений системы с коэффициентом 1, а во все остальные с коэффициентами 0. Этого можно добиться с помощью стандартной процедуры Гаусса-Жордана:

Переменные в этом случае называют базисными, а все остальные – небазисными (свободными).

Определение 4.2. Базисным решением полученной системы называется решение:

Базисное решение называется допустимым, если

Базисное решение называется невырожденным, если

Утверждение. Множество крайних точек МДР, определяемого ограничениями в задаче, соответствует множеству допустимых базисных решений системы уравнений * и при этом одному базисному решению соответствует одна крайняя точка.

Сформулируем стратегию решения задачи симплекс-методом на основании последнего утверждения:

Этап 1. Определить начальное базисное решение. Начальное базисное решение определяется по следующему правилу: за начальные базисные переменные берутся те переменные, при которых коэффициенты в уравнениях * образуют единичную матрицу

Этап 2. Переходить от одного базисного решения к другому таким образом, чтобы обеспечить максимальное возрастание функции (направленный перебор базисных решений, определяющих крайние точки МДР). Переход от одного базисного решения к другому соответствует переходу из одной вершины МДР к другой вершине в направлении возрастания функции. Пропуск вершины при этом переходе будет исключен, если состав базисных переменных будет отличаться только на одну координату. Выбор координаты, которая должна быть введена в число базисных, определяется требованием максимального прироста функции при переходе от одного решения к другому. Прирост целевой функции при введении в базис координаты  из числа небазисных характеризуется относительной оценкой  называемой симплекс-разностью.

Для решения основной или общей ЗЛП необходимо перейти к канонической задаче ЗЛП, а затем применить стратегию описанную выше. Переход к канонической задаче осуществляется введением в каждое ограничение типа неравенство дополнительной переменной, при этом правые части ограничений должны быть неотрицательны, чтобы начальное базисное решение было допустимым.

Рассмотрим теперь отдельно каждый из пунктов стратегии.

Замечание.  При решении задачи симплекс-методом ограничения на знак переменных не участвуют ни в подготовке задачи к решению, ни в самом счете.