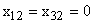4.2.2. Вычисление оптимального решения с помощью  симплекс
таблиц



 



Вид симплекс-таблицы представлен на
рисунке.



 






 



Алгоритм вычислений с
помощью симплекс-таблиц



 



 




 

  
  
 

  
1. Составить
  таблицу №1, соответствующую начальному базисному решению.

  
 

  
2. Выписать
  базисное решение. Вычислить симплекс-разности для небазисных переменных по
  формуле: , где -
  скалярное произведение.

  
Переменная,
  которой соответствует в столбце максимальная положительная симплекс-разность,
  вводится в число базисных. Соответствующий столбец пометим –   (разрешающий столбец).

  
 

  
3. Подсчитать
  величины  по формуле: , где -
  i-й элемент столбца , соответственно -  i-й элемент столбца .

  
Переменная,
  которой соответствует в строке минимальная неотрицательная величина , выводится из числа базисных. Соответствующую
  строку пометим -  (разрешающая строка).
  Элемент, стоящий на пересечении -столбца  и  -строки – разрешающий элемент  R.

  
 

  		
 





 




 

  
  
 

  
4. Построить
  новую таблицу, пересчитав предыдущую.

  
 

  
Пересчет таблицы

  
    
   
  • Заполнить
       в новой таблице: строку коэффициентов функции, столбец  и столбец .
    • 
   
  • Пересчитать
       -строку, содержащую разрешающий
       элемент, и записать в новую таблицу под тем же номером по
       формуле:      
    • 
  

  
новая строка  = старая строка  / R.

  
Полученную
  строку пометим  N.

  
 

  
    
   
  • Пересчитать
       все остальные строки таблицы и записать их под теми же номерами в
       новую таблицу по формуле:
    • 
  

  
новая строка K = старая строка K – (строка N) * КП,

  
 

  
где  КП (коэффициент пересчета) – элемент,
  стоящий на пересечении строки K
  и -столбца в старой таблице.

  
 

  
5. Повторить
  процедуру 2-4 до тех пор, пока все симплекс-разности не станут   0.

  
 

  
6. Проанализировать последнее полученное
  базисное решение.

  		
 





 



Замечания
по процедуре счёта 



 



№1. Каждая
таблица соответствует точке пересечения ограничений на графике, причем пока в
базисе есть искусственные переменные – это точки вне множества допустимых
решений.



 



№2.  В
каждой таблице при текущих базисных  переменных должны стоять столбцы единичной
матрицы.



 



№3. Столбец
 должен всегда содержать только
неотрицательные элементы.



 



Замечания
по анализу результатов счёта



 



№1. Если
в процессе решения оказалось, что среди элементов  -столбца
нет ни одного положительного, значит, задача не имеет решения вследствие
неограниченности множества допустимых решений.



 



№2. Если
в таблице, соответствующей решению задачи, в строке симплекс-разностей
содержится нулей больше, чем ограничений, значит, задача имеет бесконечное
множество решений, одно из которых найдено. 



 



№3. Если
при решении M-задачи найдено решение (все симплекс-разности 0), но в составе базисных переменных
имеется искусственная переменная, не равная нулю, то исходная задача не имеет
решения.



 



Сходимость
симплекс-метода. При условии
невырожденности базисных решений симплекс-метод сходится за конечное число
шагов.



 



 



Пример 4.5.



 



Дано:






 



Решение:



 




 

  
  
Таблица 1

  		
  
  
 

  		
  
  
2,0000

  		
  
  
3,0000

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
Cj

  		
 

 

  
  
Ciб

  		
  
  
Бп

  		
  
  
Бр

  		
  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
ri

  		
 

 

  
  
0,0000

  		
  
  
x3

  		
  
  
12,0000

  		
  
  
2,0000

  		
  
  
3,0000

  		
  
  
1,0000

  		
  
  
0,0000

  		
  
  
4,0000

  		
 

 

  
  
0,0000

  		
  
  
x4

  		
  
  
6,0000

  		
  
  
-2,0000

  		
  
  
6,0000

  		
  
  
0,0000

  		
  
  
1,0000

  		
  
  
1,0000

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
D

  		
  
  
2,0000

  		
  
  
3,0000

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
 

  		
 

 

  
  
Базисное решение

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
0,0000

  		
  
  
0,0000

  		
  
  
12,0000

  		
  
  
6,0000

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
Таблица 2

  		
  
  
 

  		
  
  
2,0000

  		
  
  
3,0000

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
Cj

  		
 

 

  
  
Ciб

  		
  
  
Бп

  		
  
  
Бр

  		
  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
ri

  		
 

 

  
  
0,0000

  		
  
  
x3

  		
  
  
9,0000

  		
  
  
3,0000

  		
  
  
0,0000

  		
  
  
1,0000

  		
  
  
-  1/2 

  		
  
  
3,0000

  		
 

 

  
  
3,0000

  		
  
  
x2

  		
  
  
1,0000

  		
  
  
-  1/3 

  		
  
  
1,0000

  		
  
  
0,0000

  		
  
  
  1/6 

  		
  
  
-3,0000

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
D

  		
  
  
3,0000

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
-0,5000

  		
  
  
 

  		
 

 

  
  
Базисное решение

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
0,0000

  		
  
  
1,0000

  		
  
  
9,0000

  		
  
  
0,0000

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
Таблица 3

  		
  
  
 

  		
  
  
2,0000

  		
  
  
3,0000

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
Cj

  		
 

 

  
  
Ciб

  		
  
  
Бп

  		
  
  
Бр

  		
  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
ri

  		
 

 

  
  
2,0000

  		
  
  
x1

  		
  
  
3,0000

  		
  
  
1,0000

  		
  
  
0,0000

  		
  
  
  1/3 

  		
  
  
-  1/6 

  		
  
  
 

  		
 

 

  
  
3,0000

  		
  
  
x2

  		
  
  
2,0000

  		
  
  
0,0000

  		
  
  
1,0000

  		
  
  
  1/9 

  		
  
  
  1/9 

  		
  
  
 

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
D

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
-1,0000

  		
  
  
0,0000

  		
  
  
 

  		
 

 

  
  
Базисное решение

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
3,0000

  		
  
  
2,0000

  		
  
  
0,0000

  		
  
  
0,0000

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 









Пример 4.6.



 



Дано:






 



Решить задачу с помощью симплекс таблиц.




 



Решение:



 




 

  
  
Таблица 1

  		
  
  
 

  		
  
  
1.0000

  		
  
  
3.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
-M

  		
  
  
Cj

  		
 

 

  
  
CiБ

  		
  
  
Бп

  		
  
  
Бр

  		
  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
x5

  		
  
  
ri

  		
 

 

  
  
0.0000

  		
  
  
x3

  		
  
  
12.0000

  		
  
  
1.0000

  		
  
  
3.0000

  		
  
  
1.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
12.0000

  		
 

 

  
  
-M

  		
  
  
x5

  		
  
  
2.0000

  		
  
  
1.0000

  		
  
  
-2.0000

  		
  
  
0.0000

  		
  
  
-1.0000

  		
  
  
1.0000

  		
  
  
2.0000

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
D

  		
  
  
M+1

  		
  
  
-2M+3

  		
  
  
0.0000

  		
  
  
-M

  		
  
  
0.0000

  		
  
  
 

  		
 

 

  
  
Базисное решение

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
x5

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
0.0000

  		
  
  
0.0000

  		
  
  
12.0000

  		
  
  
0.0000

  		
  
  
2.0000

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 





 



 




 

  
  
Таблица 2

  		
  
  
 

  		
  
  
1.0000

  		
  
  
3.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
-M

  		
  
  
Cj

  		
 

 

  
  
CiБ

  		
  
  
Бп

  		
  
  
Бр

  		
  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
x5

  		
  
  
ri

  		
 

 

  
  
0.0000

  		
  
  
x3

  		
  
  
10.0000

  		
  
  
0.0000

  		
  
  
5.0000

  		
  
  
1.0000

  		
  
  
1.0000

  		
  
  
-1.0000

  		
  
  
2.0000

  		
 

 

  
  
1.0000

  		
  
  
x1

  		
  
  
2.0000

  		
  
  
1.0000

  		
  
  
-2.0000

  		
  
  
0.0000

  		
  
  
-1.0000

  		
  
  
1.0000

  		
  
  
-1.0000

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
D

  		
  
  
0.0000

  		
  
  
5.0000

  		
  
  
0.0000

  		
  
  
1.0000

  		
  
  
-M-1

  		
  
  
 

  		
 

 

  
  
Базисное решение

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
x5

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
2.0000

  		
  
  
0.0000

  		
  
  
10.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 





 







 




 

  
  
Таблица 3

  		
  
  
 

  		
  
  
1.0000

  		
  
  
3.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
-M

  		
  
  
Cj

  		
 

 

  
  
CiБ

  		
  
  
Бп

  		
  
  
Бр

  		
  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
x5

  		
  
  
ri

  		
 

 

  
  
3.0000

  		
  
  
x2

  		
  
  
2.0000

  		
  
  
0.0000

  		
  
  
1.0000

  		
  
  
0.2000

  		
  
  
0.2000

  		
  
  
-0.2000

  		
  
  
 

  		
 

 

  
  
1.0000

  		
  
  
x1

  		
  
  
6.0000

  		
  
  
1.0000

  		
  
  
0.0000

  		
  
  
0.4000

  		
  
  
-0.6000

  		
  
  
0.6000

  		
  
  
 

  		
 

 

  
  
 

  		
  
  
 

  		
  
  
D

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
-1.0000

  		
  
  
0.0000

  		
  
  
-M

  		
  
  
 

  		
 

 

  
  
Базисное решение

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
x1

  		
  
  
x2

  		
  
  
x3

  		
  
  
x4

  		
  
  
x5

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 

 

  
  
6.0000

  		
  
  
2.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
0.0000

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
  
  
 

  		
 





Вычисления
закончены, так как все симплекс-разности не положительны.



 



Замечания
по проведенным вычислениям:



 



1. Каждая
таблица соответствует точке пересечения ограничений на графике, причем пока в
базисе есть искусственные переменные – это точки вне области допустимых
решений.



 



Так таблица №1
соответствует точке с координатами , не принадлежащей области
допустимых решений, таблица №2 – точке с координатами ,
принадлежащей области, и таблица №3 – точке ,
принадлежащей области. 



 



2. В каждой
таблице при текущих базисных  переменных должны стоят столбцы единичной
матрицы.



 



Анализ решения задачи
табличным симплекс-методом 



 



1. В таблице №3
все симплекс-разности не положительны, значит последнее базисное решение –
оптимальное.






Это решение
соответствует точке .



 



2. В состав
базисных переменных последней симплекс-таблицы не входят искусственная
переменная , значит, полученное решение
соответствует поставленной задаче.



 



3. Строка
симплекс-разностей последней симплекс-таблицы содержит три нуля, больше чем
число ограничений задачи, значит,  задача имеет бесконечное множество решений,
одно из которых найдено.



 



Ответ:
задача имеет бесконечное множество решений, одно из которых  найдено.