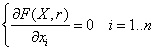7.1.1. Метод простых итераций

 

Сущность метода:

 

1. Преобразовать СЛАУ (2) к эквивалентной : , где  - квадратная матрица (),  - вектор столбец ().

2. Задать начальное приближение , как правило в качестве начального приближения выбирают .       

3. Уточнять решение согласно рекуррентному соотношению:

,                                                       (3)

что соответствует

   

4. Итерации прерываются при выполнении условия: , где - достаточно малое число – точность счета.

 

 

Для изложенной последовательности действий необходимо выяснить:

·         сходится ли процесс, т.е. имеет ли место при ;

·         какова скорость сходимости, если процесс сходится;

·         какова погрешность найденного решения, т.е. чему равна  при выполнении условия .

 

Теорема 1. (о необходимом и достаточном условии сходимости метода простых итераций)

Для сходимости  алгоритма (3) при любых  и  необходимо и достаточно, чтобы собственные значения матрицы  были по модулю меньше 1.

 

Для выяснения вопроса сходимости на основании этой теоремы  возникает необходимость вычисления собственных значений матрица, что представляет собой отдельную трудоемкую задачу.

 

Теорема 2.  (о достаточном условии сходимости метода простых итераций)

Метод простых итераций, реализующийся на основании алгоритма (3), сходится к единственному решению системы (2) при любом начальном приближении  со скоростью не медленнее геометрической прогрессии, если какая-либо норма матрицы  меньше 1.

 

Замечания.

1. Условия теоремы предъявляют завышенные требования к матрице , поэтому сходимость может быть даже при .

2. Сходящийся процесс является самоисправляющимся, т.е. ошибочное приближение можно рассматривать как новое начальное.

3. Условия сходимости  выполняются, если в исходной матрице диагональные элементы преобладают, т.е.

и хотя бы для одного уравнения неравенство строгое.

4. Чем меньше , тем быстрее сходимость метода.

 

Теорема 3.

Если в итерационном процессе норма матрицы , согласованная с нормой вектора , меньше 1, то справедлива следующая оценка погрешности:

     или     

На основании этой теоремы можно получить число итераций, требуемых для достижения заданной точности:

 

Алгоритм решения задачи методом простых итераций

 

1. Проверить достаточное условие сходимости метода. Метод сходится, если диагональные коэффициенты в левой части системы преобладают, т.е. в каждом уравнении такой коэффициент  по модулю больше, чем сумма модулей всех остальных.   Если условие не выполнено, следует привести систему к виду, при котором диагональные элементы преобладают. Для этого: найти в левой части каждого уравнения максимальный по модулю коэффициент. Если при этом он по модулю больше, чем сумма модулей всех остальных, записать уравнение в новую систему, так, чтобы этот коэффициент стал диагональным; из оставшихся после перестановки уравнений составить линейно-независимые между собой комбинации так, чтобы все строки новой системы были заполнены, и выполнялось условие преобладания диагональных элементов. При этом необходимо, чтобы все уравнения исходной системы были использованы в новой системе.   2. Разрешить первое уравнение полученной системы  относительно , второе относительно -  и т.д. В результате получается эквивалентная система .   3. Задать начальное приближение .   4. Производить вычисления по формулам: ,               , до тех пор, пока не выполнится условие окончания: . В этом случае критерий окончания может быть интерпретирован так: производить вычисления до тех пор, пока  максимальная по модулю разница между координатами решений на соседних итерациях не станет меньше .

 

 

Пример 7.1. Решить систему методом простых итераций.

 

Дано:                         

 

Решение:

 

1. Проверим условие сходимости для  заданной системы:

 

Очевидно, условие сходимости не выполнено ни для одного из уравнений системы, следовательно, необходимо преобразовать исходную систему к виду, при котором диагональные коэффициенты преобладают.

 

Преобразуем исходную систему. В данном случае достаточно переставить уравнения системы:

 

 

2. Преобразуем систему к эквивалентному виду:

 

3. Зададим начальное приближение:

 

4. Найдем решение СЛАУ  методом простых итераций с точностью

 

 

                         

  - продолжаем вычисления.

 

                       

 - продолжаем вычисления.

 

Остальные итерации запишем в виде таблицы:

 

 

Критерий окончания счета выполнен, получено решение:

 

Ответ: