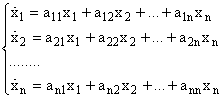7.2.2. Уточнение корней уравнения. Метод половинного деления

Пусть на отрезке отделен корень уравнения *. Отрезок называют начальным интервалом неопределенности.

Процедура уточнения корня заключается в построении последовательности вложенных друг в друга отрезков, каждый из которых содержит корень уравнения. Для этого находится середина текущего интервала неопределенности и в качестве следующего интервала неопределенности выбирается та половина отрезка, для которой функция на концах имеет разные знаки.

Процедура деления отрезка пополам заканчивается, когда длина текущего интервала неопределенности становится меньше заданной величины . За значение корня берется середина последнего интервала неопределенности.

Алгоритм метода половинного деления

Метод имеет линейную, но безусловную сходимость. Его погрешность за каждую итерацию уменьшается вдвое. Недостатком метода является то, что он не может использоваться для нахождения корней четной кратности.

Пример 7.4. Уточнить корень уравнения:  на отрезке  методом половинного деления. Точность счета

Решение:

Оформим решение в виде таблицы:

Получено решение