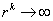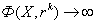7.2.4. Уточнение корней. Метод простых итераций

Процедура нахождения корня  методом простых итераций заключается в замене уравнения * равносильным вида , и  использовании затем рекуррентного соотношения  для уточнения корня.

Задача, таким образом, сводится к нахождению абсциссы точки пересечения прямой и кривой .

Рассмотрим два случая преобразования уравнения * к равносильному виду: и

Сходящийся процесс простых итераций

Расходящийся процесс простых итераций

Как видно из чертежа в первом случае получен сходящийся процесс, а во втором расходящийся.

Т.о. преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия .

Теорема (о достаточном условии сходимости метода простых итераций)

Пусть выполнены условия:

·         функция имеет производные для всех ;

·         существует число , такое, что  для всех .

Тогда последовательность, определяемая алгоритмом , сходится к решению уравнения *, т.е. при .

Алгоритм метода простых итераций

Замечание. В качестве эквивалентного преобразования исходного уравнения можно взять следующее:

Пример 7.6. Уточнить корень уравнения:  на отрезке  методом итераций. Точность счета

Решение:

1.  Преобразуем уравнение к эквивалентному виду:  и подберём коэффициент , так чтобы условие сходимости выполнялось.

Для этого найдём производную функции : . Положим , построим график полученной функции  и исследуем ее на отрезке .

Как видно из графика условия сходимости метода выполнено.

2. Возьмём .

3. Вычислим первое приближение корня:

Вычислим второе приближение корня:

Получено решение