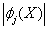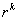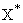7.4. Аппроксимация сеточных функций

На практике часто бывает, что заданный порядок m приближающего многочлена  значительно меньше числа узлов . В этом случае интерполирование, вообще говоря, становится невозможным и приходится прибегать к иным приемам построения приближающих многочленов. Обычно здесь используют точечный метод наименьших квадратов. Согласно этому способу, за меру отклонения многочлена  от данной функции на множестве точек  принимают величину:

, где ,

равную сумме квадратов отклонений многочлена от функции )  на заданной системе точек.  - это функция коэффициентов , эти коэффициенты надо подобрать так, чтобы величина  была наименьшей. Полученный многочлен называют аппроксимирующим для данной функции, а процесс построения этого многочлена - точечной квадратичной аппроксимацией функции. График многочлена  при заданной степени  не обязательно проходит через заданные точки

Для решения задачи точечной квадратичной аппроксимации найдем частные производные от функции  по всем переменным .

Приравнивая эти производные нулю, получим для определения неизвестных  систему  уравнений с  неизвестными.

Можно показать, что коэффициенты  могут быть найдены из системы:

где       ;       ;

      ;

Можно доказать, что если среди точек  нет совпадающих и , то определитель системы отличен от нуля, и, следовательно эта система имеет единственное решение.

Многочлен с коэффициентами , полученными как решение системы, обладает минимальным квадратичным отклонением.

Замечание. Если , то аппроксимирующий многочлен  совпадает с многочленом Лагранжа для системы точек . 

Обычно для удобства необходимые величины вычисляют по таблице :

Пример 7.9.

Построить аппроксимирующий многочлен 1-го порядка

Дано: функция, заданная таблично:

Решение:

Будем искать многочлен

Коэффициенты системы для определения .

Составим таблицу:

Тогда: