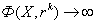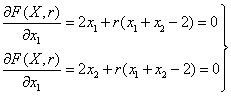2.3.5.1. Метод вариации произвольной постоянной (метод Лагранжа)










2.3.5.1. Метод вариации произвольной постоянной (метод Лагранжа)



Дано:




 



Найдем сначала
решение соответствующего линейного однородного ДУ:  - это ДУ с разделяющимися переменными.






Будем искать
решение неоднородного линейного ДУ в виде , предварительно представив произвольную
постоянную  как
неизвестную функцию :
.



Подстановка  в исходное ДУ, должна
обратить последнее в верное тождество:















Окончательно: 



Метод позволяет
свести решение неоднородного линейного ДУ к решению двух ДУ с разделяющимися
переменными.



 



Алгоритм решения линейного
неоднородного ДУ методом вариации произвольной постоянной






 



1. Привести уравнение к виду *, указать тип уравнения.



2. Записать соответствующее однородное ДУ 1-го порядка: . Это уравнение
является уравнением с разделяющимися переменными.



3. Решить полученное однородное уравнение, записать его решение в
виде: .



4. В полученном решении заменить произвольную постоянную  на неизвестную функцию
.



5. Подставить решение из п.4. в уравнение *, и выразить из
него 



6. Найти : .



7. Подставить найденное выражение для в решение из п. 4. Это – решение
исходного линейного уравнения.



8. Проверить возможно потерянные решения.



9. Записать в ответ общее решение ДУ.



 






 







Пример 2.5.



Дано:




Решение:



1. Выразим старшую производную: 



Правая часть ДУ имеет вид: , где , , 



значит данное ДУ является линейным
неоднородным 1-го порядка.



2. Запишем соответствующее линейное
однородное ДУ (ЛОДУ):  - это ДУ является ДУ с разделяющимися
переменными.



 



3. Решаем ЛОДУ:



                                                          



                                    - решение ЛОДУ



4. Заменим произвольную постоянную
на неизвестную функцию:






5. Найдем производную найденного
решения: 



Подставим найденные выражения в ДУ
из п.1:









                         






6. Найдем функцию : 



7. Подставим найденное выражение в
решение из п.4:  -
решение линейного ДУ.



8. Потерянных решений нет.



9.
Ответ: