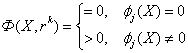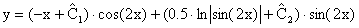2.4. Дифференциальные уравнения 1-го порядка, неразрешенные относительно производной

ДУ 1-го порядка неразрешенное относительно производной характеризуется тем, что из него не может быть легко выражена производная .

Одним из методов решения таких уравнений является применение математических преобразований, целью которых является выражение производной из ДУ. В результате получается одно или несколько ДУ вида: 

Пример.

Дано:

Решение:

Выделим полный квадрат в левой и правой частях уравнения:

и         

Получили два ДУ, разрешенных относительно производной:

1)                - ДУ с разделяющимися переменными    

2)        - линейное неоднородное ДУ

При интегрировании ДУ получаем , при интегрировании ДУ  получаем .

Ответ: ,     

В общем случае алгоритмических методов решения ДУ, неразрешенных относительно производной, не существует, кроме случаев, когда из ДУ легко выражается  или . В этом случае используют метод введения параметра.

2.4.1. Метод  введения параметра

Пример 2.9.

Дано:

Решение:

1. Данное ДУ неразрешено относительно , но разрешено относительно :

2. Введем параметр , получим:

3. Возьмем полный дифференциал левой и правой части уравнения:

4. Сделаем замену , получим:

- получили ДУ с разделяющимися переменными

5. Решаем ДУ:

    - решение ДУ с разделяющимися переменными

6. Запишем решение исходного ДУ в параметрической форме:

7. Проверяем возможно потерянные решения:      

Подставляем  в исходное ДУ:           

В полученном выражении левая часть равна правой (тождество), значит  - решение ДУ.

8. Ответ:

В данном примере можно исключить параметр и получить решение в явном виде. Для этого выразим парметр из первого уравнения:

Затем подставим полученное выражение во второе уравнение: .

Ответ: