2.4.2. Особые решения дифференциального уравнения

Определение 2.10. Решение уравнения называется особым, если через каждую его точку, кроме этого решения, проходит и другое решение, имеющее в этой точке ту же касательную, что и решение , но не совпадающее с ним в сколь угодно малой окрестности этой точки.

Если функция  и производные  и непрерывны, то любое особое решение уравнения  удовлетворяет также уравнению .

Чтобы отыскать особые решения уравнения, надо:

1) составить систему: ;

2) исключить из системы , получится уравнение  - уравнение дискриминантной  кривой;

3) для каждой ветви дискриминантной кривой проверить является ли эта ветвь решением уравнения, и, если является, то будет ли решение особым, т.е. касаются ли его в каждой точке другие решения.

Пример 2.10.

Дано:

Найти особые решения уравнения.

Решение:

1. Запишем ДУ в виде :

Найдем .

Составим систему: .

2. Исключим из системы . Для этого выразим из второго уравнения  и подставим в первое:

             - уравнение дискриминантной кривой.

3. Проверим, будет ли найденная кривая особым решением. Для этого сначала проверяем, является ли она решением уравнения.  Для этого подставляем  в исходное ДУ:

      .

В полученном выражении левая часть равна правой (тождество), значит  - решение ДУ. (см. пример 2.9)

Теперь проверяем, является ли это решение особым. В примере 2.9 были найдены другие решения ДУ: .

Запишем условия касания кривых  и в точке с абсциссой :

1) ;

2) .

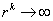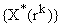Получим, т.к.  (из 2), то , а значит   (из 1) или , что справедливо для любого . Значит, при каждом  решение  в точке с абсциссой  касается одной из кривых семейства  (при ), не совпадающей с ним, значит это решение особое.