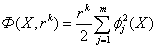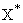3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ

Дифференциальное уравнение -го порядка в общем случае имеет вид:

или

   - уравнение, разрешенное относительно производной.

Решение ДУ имеет вид  и зависит от произвольных постоянных:

3.1. Условия существования и единственности решения дифференциальных уравнений высших порядков

Определение 3.1. Задачей Коши для ДУ называется задача об отыскании частного решения ДУ, удовлетворяющего начальным условиям, где  - порядок ДУ.

Определение 3.2. Начальные условия – это условия на функцию  и ее производные до  порядка включительно, заданные в одной и той же точке , называемой начальной.

Поставить задачу Коши для ДУ это значит задать начальные условия.

Пример.  Записать ДУ 4-го порядка в общем виде. Поставить задачу Коши.

Теорема Коши. (Теорема существования и единственности решения ДУ)

Дано:

Если в некоторой области  , содержащей точку , функция  является непрерывной функцией своих аргументов и удовлетворяет условию Липшица по всем аргументам, начиная со второго, то в достаточно малом интервале , существует единственное решение ДУ , удовлетворяющее начальным условиям:

Замечание: Условие Липшица может быть заменено несколько более грубыми условиями существования ограниченных частных производных первого порядка по всем аргументам, начиная с :  в области .

Утверждение:

1. Решение существует на интервале, если функция непрерывна.

2. Решение единственное в области , если существуют ограниченные непрерывные частные производные