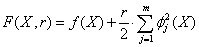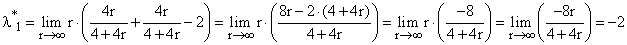(не сдан) |
4.2. Линейные однородные ДУ с постоянными коэффициентами
Определение 4.7. Линейным однородным ДУ с постоянными коэффициентами называется ДУ вида:
где –
Алгоритм решения ЛОДУ с постоянными коэффициентами
1. Составить характеристическое (ХУ) уравнение (алгебраическое):
2. Найти все 3. Найти ФСР для данного ДУ и записать решение в виде:
где каждая
функция
Правило построения ФСР а) Замечание. Корень будет простым, если среди корней встречается единственный раз.
Тогда в решение запишем 1 слагаемое вида:
б) Замечание. Корень – кратный, если среди множества корней встречается более 1 раза (k раз).
Тогда в решение запишем k слагаемых вида:
в) здесь Замечание. Комплексно-сопряженные корни будут простыми,
если корень вида
Тогда в решение запишем 2 слагаемых:
г) Замечание. Комплексно-сопряженные
корни будут кратными, если корень вида
Тогда в решение запишем 2k слагаемых:
Дано:
Решение:
1.
Составим характеристическое уравнение: Это квадратное уравнение, вида 2. Решим характеристическое уравнение:
3. Запишем решение ЛОДУ:
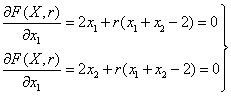 
Получим:
Ответ: Пример 4.2. Дано:
Решение: 1.
Составим характеристическое уравнение: 2. Решим характеристическое уравнение:
3. Запишем решение ЛОДУ:
Эти
корни кратные (совпадающие), кратность (число совпадений) Получим:
Ответ: Дано:
Решение:
1.
Составим характеристическое уравнение: 2. Решим характеристическое уравнение:
3. Запишем решение ЛОДУ:
Получим:
Ответ: Пример 4.4. Дано:
Решение:
1.
Составим характеристическое уравнение: 2. Решим характеристическое уравнение:
Решаем Решаем Замена:
Получили:
3. Запишем решение ЛОДУ:
Эти корни
кратные (совпадающие), кратность (число совпадений)
Эти корни
кратные (совпадающие), кратность (число совпадений)
Эти корни
кратные (совпадающие), кратность (число совпадений) Получим:
Ответ: |

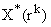 –
пара простых комплексно-сопряженных корней,
–
пара простых комплексно-сопряженных корней, 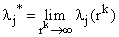 –
пара кратных комплексно-сопряженных корней (кратности k)
–
пара кратных комплексно-сопряженных корней (кратности k)