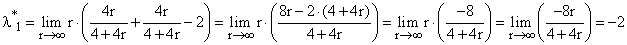4.3. Линейные неоднородные ДУ с постоянными коэффициентами (ЛНДУ)
Определение 4.6. Линейным неоднородным ДУ с постоянными коэффициентами называется ДУ вида:
где –
Теорема о структуре общего решения неоднородного уравнения Общее решение
неоднородного уравнения представляется суммой общего решение соответствующего
однородного уравнения 4.3.1. Решение ЛНДУ методом вариации произвольных постоянных
Алгоритм решения ЛНДУ методом вариации произвольных постоянных
1. Решить ЛОДУ с той же левой частью, записать его общее решение.
2. В полученном решении заменить произвольные постоянные на неизвестные функции
3. Составить систему:
Это система алгебраических уравнений, здесь
неизвестными являются 4. Решить систему, найти: 5. Найти
6. Подставить полученные выражения в решение из п. 2. Получится решение ЛНДУ.
Дано:
Решение:
1. Решаем ЛОДУ с той же левой частью:
2. Заменим в полученном решении произвольные постоянные на неизвестные функции:
3. Составим систему уравнений:
4. Решаем систему:
Из
первого уравнения: Подставим во второе уравнение:
4. Найдем неизвестные функции:
5. Подставим в решение из п. 2:
Ответ:
Дано:
Решение:
1. Решаем ЛОДУ с той же левой
частью:
2. Заменим в полученном решении произвольные постоянные на неизвестные функции:
3. Составим систему уравнений:
4. Решаем систему:
Из
первого уравнения: Подставим
во второе уравнение:
4. Найдем неизвестные функции:
5. Подставим в решение из п. 2:
Ответ:
|
действительные числа.
и частных решений неоднородного
уравнения, соответствующих неоднородности.
.
, проинтегрировав 
:
, тогда 
- решение ЛНДУ
, тогда 
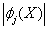
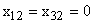
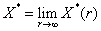
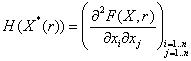
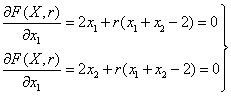- решение ЛНДУ