Дифференциальные уравнения
4.3.2. Метод подбора частного решения для ЛНДУ со специальной правой частью
(не сдан) |
4.3.2. Метод подбора частного решения для ЛНДУ со специальной правой частью
В случаях, когда правая часть ЛНДУ имеет специальный вид: Рассмотрим
подробнее структуру слагаемых правой части ДУ:
Примеры функций
Алгоритм решение ЛНДУ со специальной правой частью методом подбора частного решения
1. Решить ЛОДУ с той же левой частью, записать его общее решение.
2. Для каждого слагаемого в правой части уравнения выписать параметры:
3. Сгруппировать слагаемые с одинаковыми
4. Для каждой выделенной группы записать структуру частного решения по следующему правилу: а) если
б) если
5. Определить значения неизвестных коэффициентов 5.1. Подставить вместо 5.2. Привести подобные слагаемые в левой и правой частях полученного уравнения. 5.3. Приравнять коэффициенты при одинаковых
функциях 5.4. Решить систему, найти коэффициенты 5.5. Полностью записать частное решение.
6. Записать решение ЛНДУ:
Замечание. Если
задание сформулировано следующим образом «Определить структуру общего решения
ЛНДУ методом подбора частного решения», то выполняются пункты 1-4 и 6
алгоритма, при этом в решении остаются неопределенными коэффициенты
Дано: Решение: 1. Решаем соответствующее ЛОДУ с той же левой частью:
2. Исследуем структуру правой части ЛНДУ:
3. Так как
4. Для каждой группы слагаемых записываем частное решение: Первое частное решение:
Окончательно:
Второе частное решение:
Окончательно: 6. Записываем структуру общего
решения ЛНДУ:
Ответ:
Дано: Решение: 1. Решаем соответствующее ЛОДУ с той же левой частью:
2. Исследуем структуру правой части ЛНДУ:
3. Группируем слагаемые с
одинаковыми параметрами
4. Для каждой группы слагаемых записываем частное решение: Первое частное решение:
Окончательно:
Второе частное решение:
Окончательно: 6. Записываем структуру общего
решения ЛНДУ:
Ответ:
Дано:
Решение: 1. Решаем соответствующее ЛОДУ с той же левой частью:
2. Исследуем структуру правой части ЛНДУ:
3. Группируем слагаемые с
одинаковыми параметрами
4. Для полученной группы слагаемых записываем частное решение: Частное решение:
Окончательно:
5. Находим неизвестные коэффициенты частного решения методом неопределенных коэффициентов:
Приравниваем коэффициенты при
одинаковых степенях
Из полученной системы находим:
Окончательно:
Проверка:
6. Записываем решение ЛНДУ:
Ответ: |

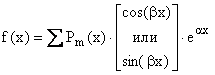 может быть применен
метод подбора частного решения.
может быть применен
метод подбора частного решения. 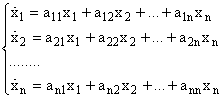 , здесь
, здесь 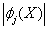 - необязательный
множитель
- необязательный
множитель