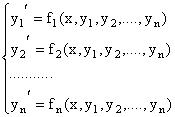5. СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ (СДУ)

Рассмотрим движение материальной точки в пространстве под действием силы , где - вектор-функция, определяющая положение точки в пространстве,  - вектор-функция скорости, - время.

Для описания движения используется математическая модель, выраженная ДУ:

Если спроектировать это векторное уравнения на оси неподвижной системы координат, то оно может быть заменено тремя скалярными уравнениями, объединенными в систему:

Определение 5.1. Системой дифференциальных уравнений (СДУ) называется совокупность дифференциальных уравнений, в каждое из которых входят: независимая переменная, неизвестные функции и производные неизвестных функций.

В рассмотренном примере:

                       - независимая переменная

   - неизвестные функции

                - производные этих функций

Будем рассматривать СДУ число уравнений, которых равно числу неизвестных функций.

Определение 5.2. Порядок СДУ определяется суммой порядков её уравнений.

Определение 5.3. Решением СДУ называется такая совокупность функций, которые при подстановке в каждое уравнение системы обращают его в тождество.

Если в примере о движении материальной точки за неизвестные функции считать не только координаты , но и проекции скоростей , то тогда получим:

Особенностью данной системы является то, что все её уравнения 1-го порядка, разрешенные относительно производной.

Определение 5.4. Нормальной СДУ называется система, состоящая из ДУ 1-го порядка, разрешенных относительно производной.

Нормальная СДУ имеет вид:

Порядок нормальной системы определяется количеством её уравнений.

Переход от ДУ n-го порядка к нормальной системе