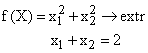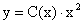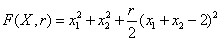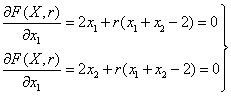5.2. Системы линейных неоднородных ДУ с постоянными коэффициентами (СЛНДУ)Определение 5.6. Системой линейных неоднородных
дифференциальных уравнений с постоянными коэффициентами (СЛНДУ)
Решение СЛНДУ
может быть найдено методом вариации произвольных постоянных, а в случае, если
функции
5.2.1. Решение СЛНДУ методом вариации произвольных постоянных
Алгоритм решение СЛНДУ методом вариации произвольных постоянных 1. Решить соответствующую СЛОДУ, записать её общее решение.
2. В полученном решении заменить произвольные
постоянные
3. Подставить полученное решение в исходную
СЛНДУ, получится система алгебраических уравнений относительно
4. Решить систему, найти:
5. Найти
6. Подставить полученные выражения в решение из п. 2. Получится решение СЛНДУ. Пример 5.5. Дано: Решить СЛНДУ методом вариации произвольных постоянных.
Решение: 1. Решаем ЛОДУ вида: Составим матрицу коэффициентов
системы: Составим матрицу Составим
характеристическое уравнение
Найдем собственные вектора матрицы и запишем решение СЛОДУ:
Запишем решение системы в скалярной форме:
2. В полученном решении заменим произвольные постоянные на неизвестные функции:
3. Подставим полученное решение в исходную СЛНДУ. Для этого найдем сначала
производные
После подстановки получим:
4. Решаем систему:
5. Найдем функции
6. Подставим найденные функции в решение из пункта 2:
Получим:
Ответ: |
-го порядка называется
СДУ вида:
имеют
специальный вид – методом подбора частного решения.
на
неизвестные функции 
.
:
и найдем собственные значения матрицы:
, 
. Собственные значения матрицы –
корни характеристического уравнения – простые, действительные.
и
: 
.
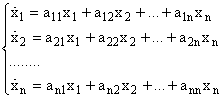
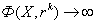
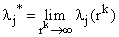
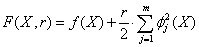
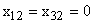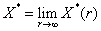- система
алгебраических уравнений с неизвестными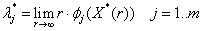 
и 
.
.
и 
:
