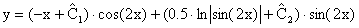Дифференциальные уравнения
5.2.2 Решение СЛНДУ со специальными правыми частями методом подбора частного решения
(не сдан) |
5.2.2 Решение СЛНДУ со специальными правыми частями методом подбора частного решения
В случаях, когда правые части уравнений СЛНДУ имеют специальный вид: Рассмотрим
подробнее структуру слагаемых правой части ДУ:
Алгоритм решение СЛНДУ со специальными правыми частями методом подбора частного решения 1. Решить соответствующую СЛОДУ, записать её общее решение.
2. Для каждого слагаемого в правой части каждого уравнения выписать параметры:
3. Сгруппировать слагаемые с одинаковыми
4. Сгруппировать слагаемые с одинаковыми 5. Для каждой выделенной группы записать структуру частного решения по следующему правилу: а) если
б) если
6. Определить значения неизвестных коэффициентов методом неопределенных коэффициентов.
7. Записать решение СЛНДУ как сумму решения СЛОДУ и всех частных
Пример 5.6. Дано: Решить СЛНДУ методом подбора частного решения.
Решение: 1. Решаем ЛОДУ вида: Она имеет решение вида:
2. Исследуем структуру неоднородности в каждом уравнении исходной системы. Первое уравнение не содержит неоднородности. Второе уравнение содержит
неоднородность
3,4. Группировки по уравнениям нет.
5. Сформируем столбец частного
решения по параметрам:
Тогда
6. Найдем значения Для этого найдем сначала
производные
Подставим найденные функции в исходную систему:
Окончательно:
7. Получим:
Ответ: |

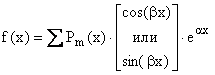 может быть применен
метод подбора частного решения.
может быть применен
метод подбора частного решения. 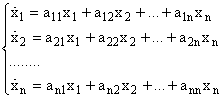 , здесь
, здесь 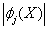 - необязательный
множитель
- необязательный
множитель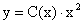
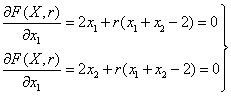 (см. пример 5.5.)
(см. пример 5.5.)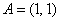 или
или 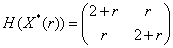 .
.