(не сдан) |
6.1. Простейшие типы точек покоя
Исследуем
расположение траекторий в окрестности точки покоя Для отыскания решения системы составляем характеристическое уравнение:
Корни характеристического уравнения позволяют исследовать точку покоя на устойчивость.
6.1.1. Правило определения устойчивости СЛОДУ
Если действительные части всех корней характеристического уравнения системы отрицательны, то тривиальное решение (точка покоя) асимптотически устойчиво.
Если же
действительная часть хотя бы одного корня положительна, то соответствующее
этому корню решение при сколь угодно малых по модулю значениях Эти утверждения справедливы и для системы ЛОДУ с постоянными
коэффициентами |

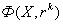 ,
, 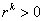
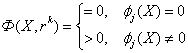 или
или