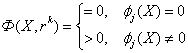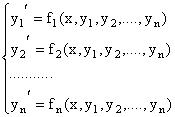6.2. Признаки отрицательности действительных частей всех корней характеристического уравнения.

Рассмотрим характеристическое уравнение для СЛОДУ –порядка:

.

Если характеристическое уравнение имеет высокую степень,  то его решение представляет значительные трудности, поэтому большое значение имеют методы, позволяющие, не решая уравнение, установить, будут ли все его корни иметь отрицательную вещественную часть.

Необходимое условие.  Все . В случае  это условие является и достаточным.

Условия Рауса-Гурвица. Необходимо и достаточно, чтобы были положительными все главные диагональные миноры матрицы Гурвица:

На главной диагонали этой матрицы стоят числа . В каждой строке индекс каждого числа на 1 меньше индекса предыдущего. Числа с индексами или  заменяются 0.

Главные диагональные миноры матрицы Гурвица имеют вид:

Условия Льенара-Шипара. Необходимо и достаточно, чтобы все , и чтобы  и т.д., где те же, что и в условиях Рауса-Гурвица.

Эти условия равносильны условиям Рауса-Гурвица, но удобнее, так как содержат меньше определителей.