(не сдан) |
7.1. Приближенно-аналитические методы решения задачи Коши7.1.1. Методы степенных рядовТеорема. Дано:
Если правая
часть ДУ, т.е. функция
7.1.1.1. Метод последовательного дифференцирования
Рассмотрим
приведенную выше задачу Коши. Будем искать решение задачи Коши для ДУ n-го
порядка в виде ряда Тейлора по степеням
Коэффициенты
ряда представляют собой производные функции Найдем их: 1) Из начальных условий определим первые n коэффициентов разложения:
2) Значение
(n+1)-го коэффициента определим, подставив в ДУ значения
3) Для нахождения всех последующих коэффициентов будем последовательно дифференцировать левую и правую часть исходного ДУ и вычислять значения коэффициентов, используя начальные условия и все уже полученные коэффициенты.
Замечание. Если выполняются условия теоремы существования и единственности решения, то частичная сумма полученного ряда Тейлора будет приближенным решением поставленной задачи Коши.
Алгоритм метода последовательного дифференцирования 1. Записать решение y(x) в виде бесконечного степенного ряда
по степеням
2. Определить значения первых n коэффициентов
3. Выразить из ДУ старшую производную. Вычислить ее значение
в начальной точке, используя начальные условия. Вычислить коэффициент
4. Продифференцировав по х выражение для старшей производной
из п. 3 найти n+1 производную функции
5. Остальные коэффициенты
6. Записать окончательное решение задачи в виде бесконечного
ряда по степеням
Пример 7.1. Дано:
Найти приближенно-аналитическое решение задачи Коши методом последовательного дифференцирования (найти 4 члена ряда).
Решение:
1. Т.к.
2. Из начальных
условий: |

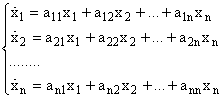
 , где
, где