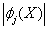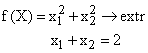|
7.1.1.2. Метод неопределенных коэффициентов
Этот метод рекомендуется применять для решения линейных ДУ, но он также может быть использован и для ДУ, содержащих неизвестную функцию и ее производные до (n-1) порядка, возведенные в целую положительную степень. Решение задачи Коши в случае использования метода ищется в виде степенного ряда:
Для отыскания
коэффициентов
Замечание.
Подстановке решения в ДУ должна предшествовать процедура представления всех
коэффициентов ДУ в виде рядов по целым неотрицательных степеням
Алгоритм метода неопределенных коэффициентов 1. Записать решение 2. Записать все входящие в ДУ производные в виде степенных
рядов по степеням
3. Выписать все коэффициенты ДУ при
4. Представить коэффициенты ДУ, являющиеся функциями x, в
виде рядов по степеням Замечание. Если в решении задачи должны быть
определены первые четыре константы
5. Подставить полученные в п. 1, 2 и 4 выражения в исходное ДУ.
6. Раскрыть скобки и привести подобные слагаемые при
одинаковых степенях
7. Приравнять коэффициенты при одинаковых степенях
8. Воспользовавшись начальными условиями определить значения
первых n констант
9. Значения остальных констант определяются из системы п. 7.
10. Записать окончательное решение задачи в виде бесконечного
ряда по степеням Пример 7.3. Дано:
Найти приближенно-аналитическое решение задачи Коши методом неопределенных коэффициентов (найти 4 члена ряда).
Решение:
1. Т.к.
2. Тогда
3. Выпишем коэффициенты дифференциального уравнения:
4. Коэффициент Представим коэффициент
|
.
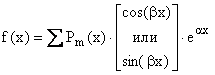необходимо
подставить данное решение в исходное ДУ и приравнять коэффициенты при
одинаковых степенях 
в
левой и правой частях уравнения.
в виде бесконечного степенного ряда по
степеням 
:
, то соответственно для корректного их
определения все бесконечные ряды в п. 1, 2 и 4 должны содержать не
меньше 4-х членов
и
т.д..
(здесь
n - порядок исходного уравнения).
, будем искать решение
задачи Коши в виде:
:
:
является конечным
рядом по степеням 
:
, аналогично: 
и 
в виде ряда по степеням 
