(не сдан) |
7.1.2. Метод последовательных приближений7.1.2.1. Случай ДУ 1-го порядкаПусть сначала дана задача Коши для ДУ 1-го порядка:
Предположим, что
в некоторой окрестности точки Будем строить
решение, интегрируя левую и правую части ДУ от
или с учетом
Это решение удовлетворяет ДУ и начальному условию. Заменяя в правой
части неизвестную функцию
затем:
Все имеющиеся приближения строятся по формуле:
Геометрически
последовательные приближения представляют собой кривые
Доказано, что
при выполнении условия Липшица, последовательные приближения Пример 7.4. Дано:
Найти приближенно-аналитическое решение задачи Коши методом последовательных приближений (сделать 4 приближения).
Решение: В
рассматриваемом примере 0-е приближение 1-е приближение 2-е приближение 3-е приближение
4-е приближение
Можно показать,
что Предел этой
суммы Можно найти аналитическое решение этой задачи, например методом вариации произвольной постоянной:
Т.о. решение, полученное методом последовательных приближений, совпало с аналитическим.
|

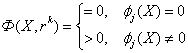
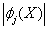
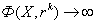
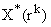 ,
,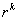 .
.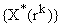
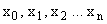
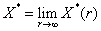
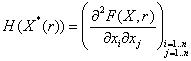
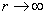
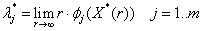
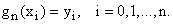
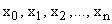 .
. 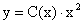 , а
, а 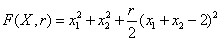 .
.