(не сдан) |
5.1.2. Метод Эйлера решения СЛОДУ
1. Составить матрицу системы: 2. Составить характеристическое (ХУ) уравнение: 3. Проанализировать корни Для каждого простого действительного
корня 3.1. Составить матрицу 3.2. Найти собственный вектор матрицы Замечание. 3.3. Записать частное решение системы в векторной
форме:
Для каждого пары простых
комплексно-сопряженных корней 3.1. Выбрать любой из двух корней, либо 3.2. Составить матрицу 3.3. Найти собственный вектор матрицы 3.4. Если был выбран корень Если был выбран корень Выделить в полученном произведении действительную 3.5. Записать частное решение системы в векторной
форме: Для каждого кратного действительного
корня 3.1. Составить матрицу 3.2. Найти все линейно-независимые
собственные векторы, соответствующие корню Если их количество
Если количество линейно-независимых собственных векторов 3.3. Записать частные решения системы в виде: 3.4. Найти соотношения для коэффициентов 3.5. Положить любые 3.6. Окончательно записать частное решение системы. 4. Записать общее решение СЛОДУ в виде суммы всех частных. Дано:
Решение: 1. Составим матрицу коэффициентов системы:
2. Составим матрицу
Составим характеристическое
уравнение Найдем определитель:
Приравняем полученный определитель
к нулю: Найдем собственные значения матрицы, решив уравнение:
Собственные значения матрицы – корни характеристического уравнения – простые, действительные. 3. Запишем
матрицу
Найдем собственный вектор Т.к. уравнения в системе линейно-зависимы, найдем ее любое ненулевое решение: Пусть Окончательно:
Запишем матрицу
Найдем собственный вектор Т.к. уравнения в системе линейно-зависимы, найдем ее любое ненулевое решение: Пусть Окончательно:
4. Запишем решение системы в векторной форме:
Запишем решение системы в скалярной форме:
Ответ:
Дано:
Решение: 1. Составим матрицу коэффициентов системы:
2. Составим матрицу
Составим характеристическое
уравнение Найдем определитель:
Приравняем полученный определитель
к нулю: Найдем собственные значения матрицы, решив уравнение:
Собственные значения матрицы – корни характеристического уравнения – простые, комплексно-сопряженные. 3. Т.к. корни характеристического
уравнения
Запишем
матрицу
Найдем собственный вектор Т.к. уравнения в системе линейно-зависимы, найдем ее любое ненулевое решение: Пусть Окончательно:
Рассмотрим произведение:
4. Запишем решение системы в векторной форме в виде линейной комбинации действительной и мнимой частей полученного произведения:
Запишем решение системы в скалярной форме:
Ответ:
Дано: Решение: 1. Составим матрицу коэффициентов системы:
2. Составим матрицу
Составим характеристическое
уравнение Найдем определитель:
Приравняем полученный определитель
к нулю: Найдем собственные значения матрицы, решив уравнение:
Собственные значения матрицы – корни характеристического уравнения – кратные, действительные. 3. Запишем
матрицу
Для данной матрицы найдется только один линейно-независимый собственный вектор, поэтому будем искать решение СЛОДУ в виде:
Тогда:
Подставим полученные выражения в первое уравнение системы:
Раскроем скобки и приведем подобные слагаемые в левой и правой частях уравнения:
Приравняем
коэффициенты при одинаковых функциях переменной
Подставим полученные выражения во второе уравнение системы:
Раскроем скобки и приведем подобные слагаемые в левой и правой частях уравнения:
Приравняем
коэффициенты при одинаковых функциях переменной
Объединим соотношения для отыскания коэффициентов:
Очевидно, что в
данной системе совпадают уравнения 2-е и 4-е, а также 1-е и 3-е при условии,
что Для нахождения
решения введем произвольные постоянные: Тогда:
4. Окончательно:
Ответ:
|

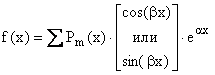
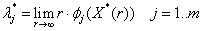





 Окончательно:
Окончательно:


